Auto MPG and Gradient Descent - My next steps
In my previous blog, I attempted prediction of MPG using my limited knowledge of data modelling techniques. My predictions were bad and model didn't work at all!!!
Remember, data modelling is new to me and it is always good start to start from bad ☺
I continued with my analysis using the next level of modelling techniques learned
Let's start the Auto MPG Data analysis.
from google.colab import files
files.upload()
import pandas as pd
autompg = pd.read_fwf( 'auto-mpg.data' , headers = None , names = [ 'mpg' , 'cylinders' , 'displacement' , 'horsepower' , 'weight' , 'acceleration' , 'model_year' , 'origin' , 'car_name' ])
print ( autompg.info() )
autompg.head()
Info method shows all columns are populated.
However, Horsepower data seems to be float but Info method shows it is an Object. So, there must be some non float values. Let's find out what they are?
for h in horsepower:
try:
f = float(h)
except ValueError:
print ( h )
As above, we see there are 6 records that have ? in horsepower. Hence, the info method showed the data type of horsepower as object.
Let's find out what these records are
autompg[ autompg['horsepower'] == '?' ]
Ok, we have now identified the records causing the horsepower to show as Object.
We can either delete these records and convert the type to float to continue with our data analysis.
However, I don't want to loose the other vital data we have. So, let's infill the horsepower and then convert to float.
We can find out the mean of horsepower and infill. However, I am going to take different approach. Find out mean of respective car make (which we can infer from car_name) and use this mean to infill
autompg.loc [ ( autompg['car_name'].str.contains ( 'ford') ) & ( autompg['horsepower'] == '?' ) , ['horsepower'] ] = round ( autompg[ ( autompg['car_name'].str.contains ( 'ford') ) & ( autompg['horsepower'] != '?' ) ].horsepower.astype(float).mean() )
autompg.loc [ ( autompg['car_name'].str.contains ( 'renault') ) & ( autompg['horsepower'] == '?' ) , ['horsepower'] ] = round ( autompg[ ( autompg['car_name'].str.contains ( 'renault') ) & ( autompg['horsepower'] != '?' ) ].horsepower.astype(float).mean() )
autompg.loc [ ( autompg['car_name'].str.contains ( 'amc') ) & ( autompg['horsepower'] == '?' ) , ['horsepower'] ] = round ( autompg[ ( autompg['car_name'].str.contains ( 'amc') ) & ( autompg['horsepower'] != '?' ) ].horsepower.astype(float).mean() )
Now, all the ? are infilled with respective means. Let's find out any records still have ? in horsepower.
autompg.loc [ autompg['horsepower'] == '?']
The above command resulted in no rows. So, we have successfully infilled the horsepower feature
Let's start the data analysis. We will use seaborn to generate heat map to understand the correlation between mpg and other features
import matplotlib.pyplot as plt
correlation_matrix = autompg.corr().round(2)
fig, ax = plt.subplots( figsize = (8,8 ))
sbn.heatmap( correlation_matrix , annot = True)
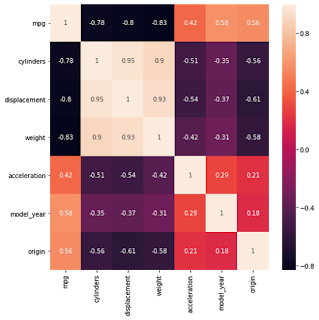
As we can see from heatmap, mpg is negatively correlated to displacement, weight and cylinders & positively correlated to acceleration , model_year and origin
So, our model should be built using some or all of these 6 features.
We will start with 1 variable, find the equation , evaluate the model and then add other features step by step until we find out the optimal equation
Let's first split the autompg model into train and test datasets
import numpy as np
testidx = set ( np.random.randint( 0 , 397 , size=98 ) )
trainidx = set (np.arange(0,397)).difference(testidx)
autompg_train = autompg.iloc [ list(trainidx) ]
autompg_test = autompg.iloc [list(testidx)]
autompg_train.info()
Let's start with our regression model.
We will first choose weight as the only input feature and come up with model.
Why I chose weight is, it is the feature that had significant correlation to mpg (although it was negative correlation)
Our equation should then be of the form
mpg = x0 + ( x1 * weight )
Generic functions defined
def gradient_descent(X, Y, B, alpha, iterations):
cost_history = [0] * iterations
m = len(Y)
for iteration in range(iterations):
# Hypothesis Values
h = X.dot(B)
# Difference b/w Hypothesis and Actual Y
loss = h - Y
# Gradient Calculation
gradient = X.T.dot(loss) / m
# Changing Values of B using Gradient
B = B - alpha * gradient
# New Cost Value
cost = cost_function(X, Y, B)
cost_history[iteration] = cost
return B, cost_history
def cost_function ( X , Y , B ):
m = len(Y)
J = np.sum( (X.dot(B) - Y) ** 2 ) / (2 * m)
return J
Train the model
weight = autompg_train['weight'].values
mpg = autompg_train['mpg'].values
m = len(mpg)
x0 = np.ones(m)
X = np.array([x0, weight ]).T
# Set the initial beta values to 0
B = np.array([0, 0 ])
Y = np.array(mpg)
# This value of alpha is set after repeated manual iterations to
# assess the cost function
alpha = 0.0000001
initial_cost = cost_function( X, Y , B )
print ( initial_cost )
newX , cost_history = gradient_descent(X, Y, B, alpha, 100000)
cost_history[-5:]
print ( newX[0] )
print ( newX[1] )
After 100000 iterations, we come up with equation as
mpg = 0.03399411 + ( 0.00665554 * weight )
Let's apply the equation on test dataset and evaluate the model
Our approach will be the following
rename mpg as mpgorig
add a new variable mpgnew derived from the equation above
autompg_test.rename( columns={'mpg':'mpgorig'}, inplace = True )
autompg_test.head()
mpg=[]
for i,j in autompg_test.iterrows():
mpg.append( round ( newX[0] + ( newX[1] * j.weight ) , 2 ) )
autompg_test['mpgnew'] = mpg
autompg_test.head()
Let's evaluate the model using RMSE , R2 and Adjusted R2
mse = 0
rmse = 0
m = len(autompg_test)
for i,j in autompg_test.iterrows():
mse += ( ( j.mpgnew - j.mpgorig ) ** 2 )
rmse = np.sqrt( mse/m )
sst = 0
ssr = 0
mean_mpg = autompg_test['mpgorig'].mean()
for i,j in autompg_test.iterrows():
sst += ( ( j.mpgorig - mean_mpg ) ** 2 )
ssr += ( ( j.mpgorig - j.mpgnew ) ** 2 )
R2 = 1 - ( ssr/sst )
k = 1
Radj = 1 - ( (1- R2) * (m-1) / ( m - k - 1 ) )
model_eval = [ rmse , R2 , Radj ]
model_eval_hist = []
model_eval_hist.append( model_eval )
model_eval_hist
After using only the weight feature, we notice that R square is negative. Bang!!!
So, this model is not correct and mpg is not just related to weight. We have to add additional features and continue our analysis.
Let's add one positively correlated feature ( model_year ) and continue our analysis
weight = autompg_train['weight'].values
mpg = autompg_train['mpg'].values
m = len(mpg)
model_year = autompg_train['model_year'].values
x0 = np.ones(m)
X = np.array([x0, weight , model_year ]).T
# Set the initial beta values to 0
B = np.array([0, 0 , 0 ])
Y = np.array(mpg)
# This value of alpha is set after repeated manual iterations to
# assess the cost function
alpha = 0.0000001
initial_cost = cost_function( X, Y , B )
print ( initial_cost )
newX , cost_history = gradient_descent(X, Y, B, alpha, 100000)
cost_history[-5:]
print ( newX )
autompg_test.drop( columns={'mpgnew'}, inplace = True )
autompg_test.head()
mpg=[]
for i,j in autompg_test.iterrows():
mpg.append( round ( newX[0] + ( newX[1] * j.weight ) + ( newX[2] * j.model_year ) , 2 ) )
autompg_test['mpgnew'] = mpg
autompg_test.head()
def evaluate_model( nvars ):
mse = 0
rmse = 0
m = len(autompg_test)
for i,j in autompg_test.iterrows():
mse += ( ( j.mpgnew - j.mpgorig ) ** 2 )
rmse = np.sqrt( mse/m )
sst = 0
ssr = 0
mean_mpg = autompg_test['mpgorig'].mean()
for i,j in autompg_test.iterrows():
sst += ( ( j.mpgorig - mean_mpg ) ** 2 )
ssr += ( ( j.mpgorig - j.mpgnew ) ** 2 )
R2 = 1 - ( ssr/sst )
k = nvars
Radj = 1 - ( (1- R2) * (m-1) / ( m - k - 1 ) )
model_eval = [ rmse , R2 , Radj ]
model_eval_hist.append( model_eval )
print ( model_eval_hist )
evaluate_model( 2 )
model_eval_hist
After adding model_year feature to the equation, we see that R square and Adjusted R square has improved.
So, let's move on adding another feature. This time, we will add the next negatively correlated attribute ( displacement )
weight = autompg_train['weight'].values
mpg = autompg_train['mpg'].values
model_year = autompg_train['model_year'].values
displacement = autompg_train['displacement'].values
m = len(mpg)
x0 = np.ones(m)
X = np.array([x0, weight , model_year , displacement ]).T
# Set the initial beta values to 0
B = np.array([0, 0 , 0 , 0])
Y = np.array(mpg)
# This value of alpha is set after repeated manual iterations to
# assess the cost function
alpha = 0.0000001
initial_cost = cost_function( X, Y , B )
print ( initial_cost )
newX , cost_history = gradient_descent(X, Y, B, alpha, 100000)
cost_history[-5:]
autompg_test.drop( columns={'mpgnew'}, inplace = True )
mpg=[]
for i,j in autompg_test.iterrows():
mpg.append( round ( newX[0] + ( newX[1] * j.weight ) + ( newX[2] * j.model_year ) + ( newX[2] * j.displacement ) , 2 ) )
autompg_test['mpgnew'] = mpg
autompg_test.head()
evaluate_model( 3 )
After adding displacement, the model behaves badly as we can notice from adverse movement of R square and adjusted R square.
Let's take out the displacement feature but continue adding another positively correlated feature this time ( i.e., acceleration )
weight = autompg_train['weight'].values
mpg = autompg_train['mpg'].values
model_year = autompg_train['model_year'].values
acceleration = autompg_train['acceleration'].values
m = len(mpg)
x0 = np.ones(m)
X = np.array([x0, weight , model_year , acceleration ]).T
# Set the initial beta values to 0
B = np.array([0, 0 , 0 , 0])
Y = np.array(mpg)
# This value of alpha is set after repeated manual iterations to
# assess the cost function
alpha = 0.0000001
initial_cost = cost_function( X, Y , B )
print ( initial_cost )
newX , cost_history = gradient_descent(X, Y, B, alpha, 100000)
cost_history[-5:]
autompg_test.drop( columns={'mpgnew'}, inplace = True )
mpg=[]
for i,j in autompg_test.iterrows():
mpg.append( round ( newX[0] + ( newX[1] * j.weight ) + ( newX[2] * j.model_year ) + ( newX[2] * j.acceleration ) , 2 ) )
autompg_test['mpgnew'] = mpg
autompg_test.head()
evaluate_model( 3 )
After excluding displacement, we notice some improvement to the model but still the R square and adjusted R square is negative.
Let's add another positively correlated attribute and see if any improvements
weight = autompg_train['weight'].values
mpg = autompg_train['mpg'].values
model_year = autompg_train['model_year'].values
acceleration = autompg_train['acceleration'].values
origin = autompg_train['origin'].values
m = len(mpg)
x0 = np.ones(m)
X = np.array([x0, weight , model_year , acceleration , origin ]).T
# Set the initial beta values to 0
B = np.array([0, 0 , 0 , 0 , 0 ])
Y = np.array(mpg)
# This value of alpha is set after repeated manual iterations to
# assess the cost function
alpha = 0.0000001
initial_cost = cost_function( X, Y , B )
print ( initial_cost )
newX , cost_history = gradient_descent(X, Y, B, alpha, 100000)
cost_history[-5:]
#autompg_test.drop( columns={'mpgnew'}, inplace = True )
mpg=[]
for i,j in autompg_test.iterrows():
mpg.append( round ( newX[0] + ( newX[1] * j.weight ) + ( newX[2] * j.model_year ) + ( newX[3] * j.acceleration ) + ( newX[4] * j.origin ) , 2 ) )
autompg_test['mpgnew'] = mpg
autompg_test.head()
evaluate_model(4)
I think now we have reached the optimum model for the given data.
As per my analysis, mpg is dependent on weight, acceleration, model_year and origin features.
The model equation as per my analysis is
mpg = 0.00647098 + (-0.00688343 * weight ) + ( 0.55330239 * model_year ) + ( 0.12636515 * acceleration ) + ( 0.0257614 * origin )
Let's compare the predictions against actual
mpgorig = autompg_test['mpgorig'].values
mpgnew = autompg_test['mpgnew'].values
mpgdf = pd.DataFrame({ 'Actual': mpgorig , 'Predicted': mpgnew })
mpgdf = mpgdf.head(30)
mpgdf.plot( kind='bar' , figsize = (16,10) )
plt.grid(which='major', linestyle='-', linewidth='0.5', color='green')
plt.grid(which='minor', linestyle='-', linewidth='0.0', color='black')
plt.show()
MPG predictions showed 77% accuracy... A significant improvement from my earlier model.
Good to see I am stepping into the world of Data Science...☺
Remember, data modelling is new to me and it is always good start to start from bad ☺
I continued with my analysis using the next level of modelling techniques learned
Let's start the Auto MPG Data analysis.
Let's import the auto mpg raw file into colab
from google.colab import files
files.upload()
Our next step is to load the data into Pandas DataFrame
import pandas as pd
autompg = pd.read_fwf( 'auto-mpg.data' , headers = None , names = [ 'mpg' , 'cylinders' , 'displacement' , 'horsepower' , 'weight' , 'acceleration' , 'model_year' , 'origin' , 'car_name' ])
print ( autompg.info() )
autompg.head()
Info method shows all columns are populated.
However, Horsepower data seems to be float but Info method shows it is an Object. So, there must be some non float values. Let's find out what they are?
Analyze and infill horsepower
horsepower = list ( autompg['horsepower'].values )for h in horsepower:
try:
f = float(h)
except ValueError:
print ( h )
As above, we see there are 6 records that have ? in horsepower. Hence, the info method showed the data type of horsepower as object.
Let's find out what these records are
autompg[ autompg['horsepower'] == '?' ]
Ok, we have now identified the records causing the horsepower to show as Object.
We can either delete these records and convert the type to float to continue with our data analysis.
However, I don't want to loose the other vital data we have. So, let's infill the horsepower and then convert to float.
We can find out the mean of horsepower and infill. However, I am going to take different approach. Find out mean of respective car make (which we can infer from car_name) and use this mean to infill
autompg.loc [ ( autompg['car_name'].str.contains ( 'ford') ) & ( autompg['horsepower'] == '?' ) , ['horsepower'] ] = round ( autompg[ ( autompg['car_name'].str.contains ( 'ford') ) & ( autompg['horsepower'] != '?' ) ].horsepower.astype(float).mean() )
autompg.loc [ ( autompg['car_name'].str.contains ( 'renault') ) & ( autompg['horsepower'] == '?' ) , ['horsepower'] ] = round ( autompg[ ( autompg['car_name'].str.contains ( 'renault') ) & ( autompg['horsepower'] != '?' ) ].horsepower.astype(float).mean() )
autompg.loc [ ( autompg['car_name'].str.contains ( 'amc') ) & ( autompg['horsepower'] == '?' ) , ['horsepower'] ] = round ( autompg[ ( autompg['car_name'].str.contains ( 'amc') ) & ( autompg['horsepower'] != '?' ) ].horsepower.astype(float).mean() )
Now, all the ? are infilled with respective means. Let's find out any records still have ? in horsepower.
autompg.loc [ autompg['horsepower'] == '?']
The above command resulted in no rows. So, we have successfully infilled the horsepower feature
Let's start the data analysis. We will use seaborn to generate heat map to understand the correlation between mpg and other features
Understand the correlation between features
import seaborn as sbnimport matplotlib.pyplot as plt
correlation_matrix = autompg.corr().round(2)
fig, ax = plt.subplots( figsize = (8,8 ))
sbn.heatmap( correlation_matrix , annot = True)
As we can see from heatmap, mpg is negatively correlated to displacement, weight and cylinders & positively correlated to acceleration , model_year and origin
So, our model should be built using some or all of these 6 features.
We will start with 1 variable, find the equation , evaluate the model and then add other features step by step until we find out the optimal equation
Let's first split the autompg model into train and test datasets
Split and build the model recursively (i.e., adding feature 1 by 1 )
import numpy as np
testidx = set ( np.random.randint( 0 , 397 , size=98 ) )
trainidx = set (np.arange(0,397)).difference(testidx)
autompg_train = autompg.iloc [ list(trainidx) ]
autompg_test = autompg.iloc [list(testidx)]
autompg_train.info()
Let's start with our regression model.
We will first choose weight as the only input feature and come up with model.
Why I chose weight is, it is the feature that had significant correlation to mpg (although it was negative correlation)
Our equation should then be of the form
mpg = x0 + ( x1 * weight )
Generic functions defined
def gradient_descent(X, Y, B, alpha, iterations):
cost_history = [0] * iterations
m = len(Y)
for iteration in range(iterations):
# Hypothesis Values
h = X.dot(B)
# Difference b/w Hypothesis and Actual Y
loss = h - Y
# Gradient Calculation
gradient = X.T.dot(loss) / m
# Changing Values of B using Gradient
B = B - alpha * gradient
# New Cost Value
cost = cost_function(X, Y, B)
cost_history[iteration] = cost
return B, cost_history
def cost_function ( X , Y , B ):
m = len(Y)
J = np.sum( (X.dot(B) - Y) ** 2 ) / (2 * m)
return J
Train the model
weight = autompg_train['weight'].values
mpg = autompg_train['mpg'].values
m = len(mpg)
x0 = np.ones(m)
X = np.array([x0, weight ]).T
# Set the initial beta values to 0
B = np.array([0, 0 ])
Y = np.array(mpg)
# This value of alpha is set after repeated manual iterations to
# assess the cost function
alpha = 0.0000001
initial_cost = cost_function( X, Y , B )
print ( initial_cost )
newX , cost_history = gradient_descent(X, Y, B, alpha, 100000)
cost_history[-5:]
print ( newX[0] )
print ( newX[1] )
After 100000 iterations, we come up with equation as
mpg = 0.03399411 + ( 0.00665554 * weight )
Let's apply the equation on test dataset and evaluate the model
Our approach will be the following
rename mpg as mpgorig
add a new variable mpgnew derived from the equation above
autompg_test.rename( columns={'mpg':'mpgorig'}, inplace = True )
autompg_test.head()
mpg=[]
for i,j in autompg_test.iterrows():
mpg.append( round ( newX[0] + ( newX[1] * j.weight ) , 2 ) )
autompg_test['mpgnew'] = mpg
autompg_test.head()
Let's evaluate the model using RMSE , R2 and Adjusted R2
mse = 0
rmse = 0
m = len(autompg_test)
for i,j in autompg_test.iterrows():
mse += ( ( j.mpgnew - j.mpgorig ) ** 2 )
rmse = np.sqrt( mse/m )
sst = 0
ssr = 0
mean_mpg = autompg_test['mpgorig'].mean()
for i,j in autompg_test.iterrows():
sst += ( ( j.mpgorig - mean_mpg ) ** 2 )
ssr += ( ( j.mpgorig - j.mpgnew ) ** 2 )
R2 = 1 - ( ssr/sst )
k = 1
Radj = 1 - ( (1- R2) * (m-1) / ( m - k - 1 ) )
model_eval = [ rmse , R2 , Radj ]
model_eval_hist = []
model_eval_hist.append( model_eval )
model_eval_hist
After using only the weight feature, we notice that R square is negative. Bang!!!
So, this model is not correct and mpg is not just related to weight. We have to add additional features and continue our analysis.
Let's add one positively correlated feature ( model_year ) and continue our analysis
weight = autompg_train['weight'].values
mpg = autompg_train['mpg'].values
m = len(mpg)
model_year = autompg_train['model_year'].values
x0 = np.ones(m)
X = np.array([x0, weight , model_year ]).T
# Set the initial beta values to 0
B = np.array([0, 0 , 0 ])
Y = np.array(mpg)
# This value of alpha is set after repeated manual iterations to
# assess the cost function
alpha = 0.0000001
initial_cost = cost_function( X, Y , B )
print ( initial_cost )
newX , cost_history = gradient_descent(X, Y, B, alpha, 100000)
cost_history[-5:]
print ( newX )
autompg_test.drop( columns={'mpgnew'}, inplace = True )
autompg_test.head()
mpg=[]
for i,j in autompg_test.iterrows():
mpg.append( round ( newX[0] + ( newX[1] * j.weight ) + ( newX[2] * j.model_year ) , 2 ) )
autompg_test['mpgnew'] = mpg
autompg_test.head()
def evaluate_model( nvars ):
mse = 0
rmse = 0
m = len(autompg_test)
for i,j in autompg_test.iterrows():
mse += ( ( j.mpgnew - j.mpgorig ) ** 2 )
rmse = np.sqrt( mse/m )
sst = 0
ssr = 0
mean_mpg = autompg_test['mpgorig'].mean()
for i,j in autompg_test.iterrows():
sst += ( ( j.mpgorig - mean_mpg ) ** 2 )
ssr += ( ( j.mpgorig - j.mpgnew ) ** 2 )
R2 = 1 - ( ssr/sst )
k = nvars
Radj = 1 - ( (1- R2) * (m-1) / ( m - k - 1 ) )
model_eval = [ rmse , R2 , Radj ]
model_eval_hist.append( model_eval )
print ( model_eval_hist )
evaluate_model( 2 )
model_eval_hist
After adding model_year feature to the equation, we see that R square and Adjusted R square has improved.
So, let's move on adding another feature. This time, we will add the next negatively correlated attribute ( displacement )
weight = autompg_train['weight'].values
mpg = autompg_train['mpg'].values
model_year = autompg_train['model_year'].values
displacement = autompg_train['displacement'].values
m = len(mpg)
x0 = np.ones(m)
X = np.array([x0, weight , model_year , displacement ]).T
# Set the initial beta values to 0
B = np.array([0, 0 , 0 , 0])
Y = np.array(mpg)
# This value of alpha is set after repeated manual iterations to
# assess the cost function
alpha = 0.0000001
initial_cost = cost_function( X, Y , B )
print ( initial_cost )
newX , cost_history = gradient_descent(X, Y, B, alpha, 100000)
cost_history[-5:]
autompg_test.drop( columns={'mpgnew'}, inplace = True )
mpg=[]
for i,j in autompg_test.iterrows():
mpg.append( round ( newX[0] + ( newX[1] * j.weight ) + ( newX[2] * j.model_year ) + ( newX[2] * j.displacement ) , 2 ) )
autompg_test['mpgnew'] = mpg
autompg_test.head()
evaluate_model( 3 )
After adding displacement, the model behaves badly as we can notice from adverse movement of R square and adjusted R square.
Let's take out the displacement feature but continue adding another positively correlated feature this time ( i.e., acceleration )
weight = autompg_train['weight'].values
mpg = autompg_train['mpg'].values
model_year = autompg_train['model_year'].values
acceleration = autompg_train['acceleration'].values
m = len(mpg)
x0 = np.ones(m)
X = np.array([x0, weight , model_year , acceleration ]).T
# Set the initial beta values to 0
B = np.array([0, 0 , 0 , 0])
Y = np.array(mpg)
# This value of alpha is set after repeated manual iterations to
# assess the cost function
alpha = 0.0000001
initial_cost = cost_function( X, Y , B )
print ( initial_cost )
newX , cost_history = gradient_descent(X, Y, B, alpha, 100000)
cost_history[-5:]
autompg_test.drop( columns={'mpgnew'}, inplace = True )
mpg=[]
for i,j in autompg_test.iterrows():
mpg.append( round ( newX[0] + ( newX[1] * j.weight ) + ( newX[2] * j.model_year ) + ( newX[2] * j.acceleration ) , 2 ) )
autompg_test['mpgnew'] = mpg
autompg_test.head()
evaluate_model( 3 )
After excluding displacement, we notice some improvement to the model but still the R square and adjusted R square is negative.
Let's add another positively correlated attribute and see if any improvements
weight = autompg_train['weight'].values
mpg = autompg_train['mpg'].values
model_year = autompg_train['model_year'].values
acceleration = autompg_train['acceleration'].values
origin = autompg_train['origin'].values
m = len(mpg)
x0 = np.ones(m)
X = np.array([x0, weight , model_year , acceleration , origin ]).T
# Set the initial beta values to 0
B = np.array([0, 0 , 0 , 0 , 0 ])
Y = np.array(mpg)
# This value of alpha is set after repeated manual iterations to
# assess the cost function
alpha = 0.0000001
initial_cost = cost_function( X, Y , B )
print ( initial_cost )
newX , cost_history = gradient_descent(X, Y, B, alpha, 100000)
cost_history[-5:]
#autompg_test.drop( columns={'mpgnew'}, inplace = True )
mpg=[]
for i,j in autompg_test.iterrows():
mpg.append( round ( newX[0] + ( newX[1] * j.weight ) + ( newX[2] * j.model_year ) + ( newX[3] * j.acceleration ) + ( newX[4] * j.origin ) , 2 ) )
autompg_test['mpgnew'] = mpg
autompg_test.head()
evaluate_model(4)
I think now we have reached the optimum model for the given data.
As per my analysis, mpg is dependent on weight, acceleration, model_year and origin features.
The model equation as per my analysis is
mpg = 0.00647098 + (-0.00688343 * weight ) + ( 0.55330239 * model_year ) + ( 0.12636515 * acceleration ) + ( 0.0257614 * origin )
Let's compare the predictions against actual
mpgorig = autompg_test['mpgorig'].values
mpgnew = autompg_test['mpgnew'].values
mpgdf = pd.DataFrame({ 'Actual': mpgorig , 'Predicted': mpgnew })
mpgdf = mpgdf.head(30)
mpgdf.plot( kind='bar' , figsize = (16,10) )
plt.grid(which='major', linestyle='-', linewidth='0.5', color='green')
plt.grid(which='minor', linestyle='-', linewidth='0.0', color='black')
plt.show()
MPG predictions showed 77% accuracy... A significant improvement from my earlier model.
Good to see I am stepping into the world of Data Science...☺


Very nice and useful.
ReplyDeleteMaybe at the end you summarise the steps in in involved..
All the best !!