Auto MPG - My first ever Blog and Machine Learning

# Auto MPG Linear Regression Model

I am always passionatte about data management and now learning Data Science and Machine learning. So far, I have started with Linear Regression and especially Gradient Descent method. I thought I will practice this method on Auto MPG data

I think the first most important step in Machine Learning is understanding the data (i.e., Exploratory Data Analysis) provided to train the model

# Step - 1 : Import the auto mpg data file
from google.colab import files
files.upload()

# Layout of Auto MPG Data

    1. mpg:           continuous
    2. cylinders:     multi-valued discrete
    3. displacement:  continuous
    4. horsepower:    continuous
    5. weight:        continuous
    6. acceleration:  continuous
    7. model year:    multi-valued discrete
    8. origin:        multi-valued discrete
    9. car name:      string (unique for each instance)

# Import the necessary libraries

# This is to plot the graphs inline within the notebook
%matplotlib inline

# Importing NUMPY and PANDAS packages
import numpy as np
import pandas as pd

# This package is to draw the graphs
import matplotlib.pyplot as plt

# Set the Graph size

plt.rcParams['figure.figsize'] = (20.0, 10.0)

# Reading the data file and print the top 5 records to ensure data is read correctly
autompg = pd.read_fwf('auto-mpg.data' , header=None , sep=' ' , names=['mpg' , 'cylinders' , 'displacement' , 'horsepower' , 'weight' , 'acceleration' , 'model_year' , 'origin' ,'car_name' ] )

# Check the shape and data of Python data frame

print(autompg.shape)
autompg.head(5)

# Let's do some data checks

autompg.info()

# INFO method shows all the data is populated which suggests no need for infilling. However, the data type of Horsepower showing as Object instead of float suggests there could be some odd values. Let's do some checks on Horse Power

h1 =  dict (autompg.horsepower.value_counts())
for i in h1.keys():
  try:
    n = float(i)
  except ValueError:
    print( "Non Integer value is " , i )

# The above check shows we have some records with horsepower set to ?
# Let's review these records
autompg[autompg.horsepower == '?']

Given there are only six records with horsepower set to ?, we can either delete these records from autompg data set or infill the horsepower.

I am inclined to infill the horsepower but take the mean from respective car make

autompg.loc [ (autompg['car_name'].str.contains('ford')) & ( autompg.horsepower == '?') , ['horsepower'] ] = round ( autompg[ (autompg['car_name'].str.contains('ford')) & ( autompg.horsepower != '?') ].horsepower.astype(float).mean() , 0 )
autompg.loc [ (autompg['car_name'].str.contains('renault')) & ( autompg.horsepower == '?') , ['horsepower'] ] = round ( autompg[ (autompg['car_name'].str.contains('renault')) & ( autompg.horsepower != '?') ].horsepower.astype(float).mean() , 0 )
autompg.loc [ (autompg['car_name'].str.contains('amc')) & ( autompg.horsepower == '?') , ['horsepower'] ] = round ( autompg[ (autompg['car_name'].str.contains('amc')) & ( autompg.horsepower != '?') ].horsepower.astype(float).mean() , 0 )

autompg[autompg.horsepower == '?']



Let's now split the Auto MPG dataset to TRAIN and TEST such that
TRAIN will have 300 records and TEST will have 98 records

# rnumbers : 98 Random numbers generated which will be used as index numbers to split TEST data
# onumbers : The remaining 300 numbers to train the model

rnumbers = list ( set( np.random.randint(1,397,size=98) ) )
onumbers = list ( set(np.arange(0,398)).difference(rnumbers) )

print ( len(rnumbers ))
print ( len(onumbers ))

# Split the autompg dataset

test = autompg.iloc[ rnumbers ]
train = autompg.iloc[onumbers]
print ( train.head() )
print ( test.head() )
print ( train.info() )
print ( test.info() )

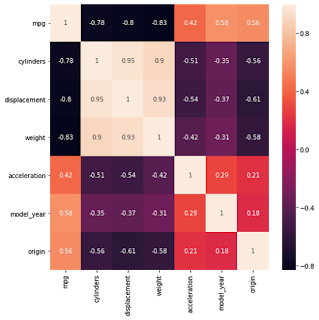
Based on what I think, MPG will be function of cylinders, displacement, horsepower, weight, accelaration.

Model Year may have little impact and Origin may not have significant impact on MPG

Let's try to check correlation of each of variables with MPG and ensure the above statement

import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (10.0, 5.0)
plt.bar(train.cylinders , train.mpg)
train.head()

plt.bar( train.horsepower.astype(float) , train.mpg )

plt.bar( train.displacement , train.mpg  )

plt.bar(train.weight , train.mpg )

plt.bar( train.acceleration , train.mpg )

plt.bar( train.mpg  , train.model_year )

plt.bar( train.origin , train.mpg )

As we can see from the above bar charts,
Origin seems to have no impact to MPG
Model Year has very little impact to MPG

So, for our modelling, we will ignore Model Year and Origin

Also, since it is my first practice Gradient Descent modelling, I am ignoring Car Name as well.

MPG = b0 + b1 * cylinders + b2 * displacement + b3 * horsepower + b4 * weight + b5 * acceleration

This will be our modelling equation.

We will now try to find optimal values for the above co efficients

First of all, let's create PANDAS series for each of Input vectors and the output vector (i.e., MPG )

cylinders = train['cylinders'].values
displacement = train['displacement'].values
horsepower = train['horsepower'].values.astype(float)
weight = train['weight'].values
acceleration = train['acceleration'].values
mpg = train['mpg'].values

m = len(displacement)
print ( m )
x0 = np.ones(m)
X = np.array([x0,  cylinders , acceleration , displacement , horsepower , weight ]).T
# Set the initial beta values to 0
B = np.array([0, 0 , 0 , 0, 0, 0 ])
Y = np.array(mpg)

# This value of alpha is set after repeated iterations to
# assess the cost function
alpha = 0.00000008

def cost_function(X, Y, B):
    m = len(Y)
    J = np.sum((X.dot(B) - Y) ** 2)/(2 * m)
    return J

inital_cost = cost_function(X, Y, B)
print(inital_cost)

def gradient_descent(X, Y, B, alpha, iterations):
    cost_history = [0] * iterations
    m = len(Y)
 
    for iteration in range(iterations):
        # Hypothesis Values
        h = X.dot(B)
        # Difference b/w Hypothesis and Actual Y
        loss = h - Y
        # Gradient Calculation
        gradient = X.T.dot(loss) / m
        # Changing Values of B using Gradient
        B = B - alpha * gradient
        # New Cost Value
        cost = cost_function(X, Y, B)
        cost_history[iteration] = cost
     
    return B, cost_history

newB, cost_history = gradient_descent(X, Y, B, alpha, 100000 )

# New Values of B
print(newB)

# Final Cost of new B
print(cost_history[-5:])

# 35.44265134 -3.15159123  0.33323164
# 12.731902691442762, 12.731896101848891, 12.731889512418512, 12.731882923151613, 12.731876334048188

# [41.67511612 -3.52509188  0.06973055]
# [12.466833967874356, 12.466833914509321, 12.46683386114959, 12.466833807795144, 12.466833754445998]

After few iterations changing the alpha value, I am stopping here my analysis and going to use the beta values obtained to do my model testing.

The reason I am stopping here is, I wanted to try Lasso and Ridge regression methods on the same data set later on

I will rename the MPG variable to MPGORIG in the TEST data set.
Will add MPGNEW variable predicted from my model and do the error analysis

test.rename( columns={'mpg':'mpgorig'}, inplace = True )
test.head()

mpg=[]

for i,j in test.iterrows():
   mpg.append(  round ( 0.01158826 + ( 0.0240618 * j.cylinders ) + ( 0.1982275 * j.acceleration ) + (-0.17026161 * j.displacement ) + (0.0814181 * float(j.horsepower) ) + ( 0.01463831 * j.weight ) , 2 )  )
         
test['mpgnew'] = mpg
test.head()
 

# Validate the model ( 1. Let's find out RMSE value )

mse =  0
rmse = 0
m = len(test)
for i,j in test.iterrows():
     mse += ( ( j.mpgnew - j.mpgorig ) ** 2 )

rmse = np.sqrt( mse/m )
print ( m )
print ( rmse )


# Validate the model ( 2. Let's find out R2 value )

sst = 0
ssr = 0
mean_mpg = test['mpgorig'].mean()

for i,j in test.iterrows():
    sst += ( ( j.mpgorig - mean_mpg ) ** 2 )
    ssr += ( ( j.mpgorig - j.mpgnew ) ** 2 )

R2 = 1 - ( ssr/sst )

print ( mean_mpg )
print ( R2 )

R2 is negative. So, the model is certainly not correct but I was only practicing the Gradient Descent Approach.

I will now move on the next modelling techniques and see if I can predict the MPG better